
ยินดีต้อนรับเข้าสู่ เว็บแทงหวยออนไลน์ 999LUCKY108 เว็บแทงหวยที่ดีที่สุดอันดับ 1 ของคนไทย
ยินดีต้อนรับลูกค้าที่น่ารักทุกท่าน เข้าสู่ระบบ เว็บแทงหวยออนไลน์ 999LUCKY เว็บแทงหวยออนไลน์ครบวงจรที่ดีที่สุด อันดับ 1 ของประเทศไทย เราเปิดบริการด้านหวยออนไลน์มายาวนานหลายปี โดยเรามีหวยออนไลน์ครบวงจรให้คุณได้เล่นมากมาย เรียกได้ว่าเว็บไซต์เราเป็นศูนย์รวมหวยออนไลน์เลยก็ว่า มีหวยทุกตัวที่ท่านต้อง อาทิเช่น หวยรัฐบาล หวยฮานอย หวยลาว Huayden หวยหุ้นไทย หวยหุ้นต่างประเทศ หวยมาเลย์ หวยปิงปอง และหวยมาแรงของเว็บ 999LUCKY อย่างเช่น หวยลัคกี้เฮง หวยที่ออกถี่่ที่สุดในบรรดาหวยออนไลน์
999lucky มีระบบการเล่นออนไลน์ที่ดีที่สุด ยังรองรับระบบ PC , browser และรวมไปถึงระบบ Android , IOS ถือว่าเว็บไซต์เราเป็นเว็บหวยออนไลน์เจ้าแรกๆ ที่ยิ่งใหญ่และทันสมัยที่สุดเลยก็ว่าได้ 999lucky ขอบอกเลยว่าเป็น เว็บหวยออนไลน์ที่ดีที่สุด จ่ายจริง ไม่เคยมีประวัติการโกงลูกค้า อัตราการจ่ายสูง และ จ่ายตามจริง โอนไว ไม่มีหัก% จ่ายเต็ม ไม่มีเลขอั้น รับทุกตัว ต้อง 999lucky ที่นี้ที่เดียวเท่านั้น
999lucky ไม่มีโกงลูกค้า แน่นอน ใครเล่นได้ก็ได้จริง โอนเงินให้จริง ฝากเงินไปแล้วปรับยอดเครดิตรวดเร็วทันใจ ฝากถอนด้วยระบบอัตโนมัติ ฝากถอนไม่มีขั่นต่ำ แทงหวยไม่มีขั่นต่ำ ถูกล้านจ่ายล้าน จ่ายจริง และระบบเรายัง ฝากถอนที่รวดเร็วที่สุด ในบรรดาเว็บหวยออนไลน์ที่เปิดให้บริการเลยก็ว่าได้ หากท่านอยากเป็น 1 ในนักเสียงโชค ที่เก่งที่สุด แนะนำให้ท่านแทงหวยกับ 999lucky เว็บ Huay ที่ดีที่สุด Hauyden เล่นแล้วรวย รวยโดยที่ท่านจะไม่รู้ตัว ก่อนใคร สมัครสมาชิก !! ฟรี ไม่เสียค่าใช้จ่ายแม้แต่บาทเดียว แล้วท่านจะไม่ผิดหวังอย่างแน่นอน บริการประทับใจ ใส่ใจดูแลตลอด 24 ชั่วโมง
999lucky เว็บหวยออนไลน์ที่ดีที่สุดอันดับ 1 ในใจคนไทย มีโปรโมชั่นและสิทธิพิเศษรอท่านอยู่ ฝากถอนไม่มีขั่นต่ำ 1 บาทก็สามารถแทงหวยได้ ต้อง 999lucky เท่านั้น อัตราจ่ายสูงสุด จ่ายจริง ไม่โกง
- ระบบฝากถอนอัตโนมัติ รวดเร็ว ทันใจ
- รองรับการแทงหวยออนไลน์เต็มรูปแบบ
- ระบบติดต่อทางทีมงานเราได้ตลอด 24 ซม.
- ระบบแนะนำสมาชิก จ่ายค่าตอบแทนสูงสุดถึง 5%
- หวยปิงปอง ออกผลด้วยตัวเองได้
- ระบบรักษาความปลอดภัยระดับเทพ
- ใช้ Cloud Server เต็มรูปแบบ
- ระบบ สำรองข้อมูลลูกค้าแบบ Ail Time ไม่ต้องกลัวว่าเงินจะหาย
- ฝากถอนได้โดยไม่มีขั่นต่ำ
- มีโปรโมชั่นปละสิทธิพิเศษอีกมากมาย
- แทงหวยไม่มีขั่นต่ำ
- อัตราการจ่ายสูงถึงบาทละ 800
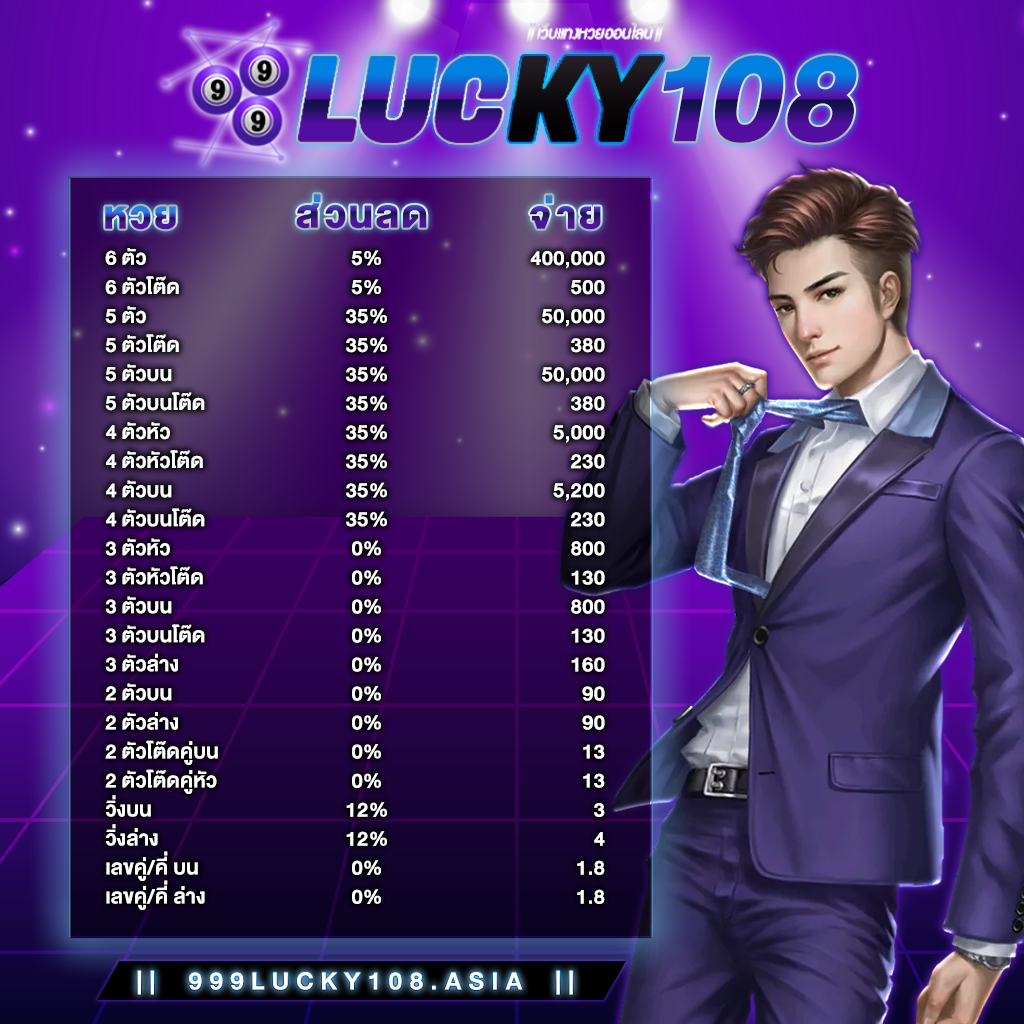
แทงหวยออนไลน์ครบวงจร ต้อง 999LUCKY ที่นี้ที่เดียวเท่านั้น ศูนย์รวมหวยออนไลน์ที่ดีที่สุด
- หวยรัฐบาลไทย
- หวยลาว
- หวยเวียดนาม
- หวยลัคกี้เฮง
- หวยปิงปอง
- หวยหุ้นไทย
- หวยหุ้นต่างประเทศ
- หวยใต้ดิน
- หวยมาเลย์
- หวยสิงคโปร์
- หวยหุ้นดาวโจนส์
999LUCKY เว็บหวยออนไลน์ที่ดีที่สุด อัตราจ่ายสูงสุด ราคาดีที่สุด จ่ายมากไม่กลัวขาดทุน
ระบบฝากถอนอัตโนมัติ ฝากถอนไม่มีขั้่นต่ำ 1 บาทก็สามารถแทงหวยได้ 999LUCKY ที่นี้ที่เดียว
999LUCKY จ่ายจริง ไม่อั้น รับทุกตัว จ่ายเต็ม ไม่มีหัก จ่ายตามจริง ถูกล้านจ่ายล้าน
หากเกิดปัญหาหรือข้อสงสัยระหว่างใช้งาน สามารถ ติดต่อทางทีมงาน เราได้ตลอด 24 ซม.
มีโปรโมชั่นและสิทธิพิเศษมากมาย รอท่านอยู่ !! แล้วท่านจะรวยไม่รู้ตัว รวยก่อนใครไปกับ 999lucky
